Language models estimate the probability distribution over sequences of tokens. Meaning that given a piece of text $\texttt{"I like pancakes"}$, a language model can give it a number, say $0.2$, therefore $p(\texttt{"I like pancakes"}) = 0.2$, which means that the sentence $\texttt{"I like pancakes"}$ is assigned a probability of $0.2$ according to the model’s estimate of the underlying distribution of the training data.

They are are canonically autoregressive (almost all the popular ones are), in which the probability of a given piece of text is estimated according to the following expression

which is the joint conditional probability of each token conditioned on previously generated tokens. Now instead of conditioning on previously generated tokens and doing that over and over again, Diffusion Language Models use the product of marginal probabilities. Marginal probability here is defined as the probability of only one token given the context.

The context here is given by $\tilde{x}$, which is a sequence with some masked tokens, leaving out a partially clean sequence. $\mathcal{M}$ is the set of positions/indices of these mask tokens.

Both of them can be used in text generation. Given a prompt, autoregressive models can keep feeding the so far generated tokens as the conditional in the conditional probability and diffusion models by appending a chunk of masked tokens at the end of the prompt.

the problem

One of the challenges of DLM training is performance gap between diffusion and autoregressive. Arguably, this is mostly because autoregressive is conditioning on more and more tokens as it goes, that is, the context $x_{<i}$ in the conditional probability $p(x_i\mid x_{<i})$ gets bigger and bigger as it goes, whereas the partially clean sequence $\tilde{x}$ in DLMs stays constant (although there are remasking strategies that tries to mitigate this problem). However, at the same time, DLMs are faster because they are generating more tokens in a single pass instead of one by one like autoregressive.

changing the probability distributions

Many research endeavors have tried closing this gap by introducing new ways to train DLMs. In the same spirit, we are trying to see if the probability distribution from which tokens are masked would give us any performance gains or if there are any behaviors worth observing with respect to them. The idea of doing this came from the idea of how marginal probability can be obtained from different amount of contexts; we then ask

During training, how much masking leads too little context and how little masking leads to too many context such that it hurts generalization

methodology

Let our training minibatch be $\mathcal{D} \in \mathcal{V}^{B \times T}$ where $B$ is batch size and $T$ is token length. As our baseline, we adopt the DLM training method of LLaDa (Nie et al., 2025), which, for each sequence $i \in \{1,2,\dots, B\}$, we sample $p_i \sim \mathrm{Uniform}(\varepsilon,1)$. And for each token $j \in \{1, 2, \dots, T\}$ we sample $r_{ij} \sim \mathrm{Uniform}(0,1)$. Tokens are masked according to the following:

Where $M$ is the probability of a token being masked. Consequently, we have $C$ which is the number of tokens masked in a sequence.

but in our study…

In our study, instead of sampling $p_i \sim \mathrm{Uniform}(\varepsilon, 1)$, we define a set of expected masking probabilities

and, for each row in the training batch, we sample

where $\alpha = w\kappa$, $\beta = (1 - w)\kappa$, and $\kappa > 0$, such that

We conduct separate experiments for each $w \in \mathbf{w}$. Which means our masking function now follows

To illustrate this, we simulate masking for each $w$ with $B = 5000$ and $T = 512$ sequences and draw a histogram ($w = \text{None}$ is the default setup).

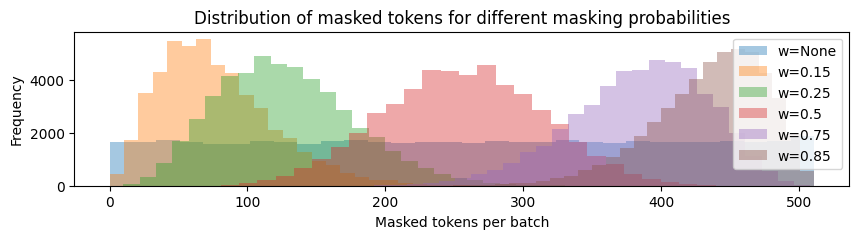
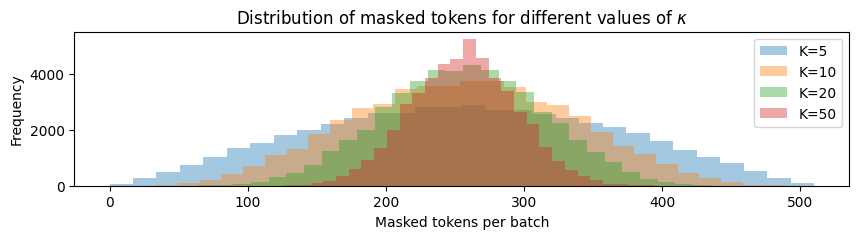
We also investigate the effect of the spread of the distribution of the masked tokens. Specifically, we control $\kappa$ which affects the variance of $C_i$

We also illustrate this using the same amount of $B$ and $T$.

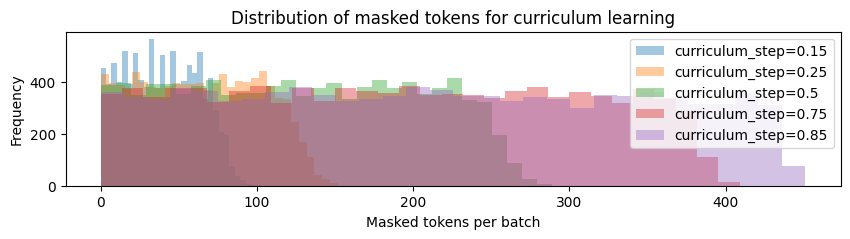
And finally, we also try to do a curriculum learning, in which the probability of masking changes depending on the training step. We set a curriculum such that the model learns to demask less tokens at the beginning but gradually changes to learning to demask more tokens. The intuition behind this is we are trying to see if a gradually shifting from easier to harder task would improve generalization. Specifically, we divide the training step budget by the number of curriculum step and use $p_i\sim \mathrm{Uniform}(\varepsilon, \mathrm{curriculum\_step})$. We set them the same as $\textbf{w}$ in our ablation experiment for the expectation. We also illustrate this curriculum training distribution

results?!

masking sweet spot

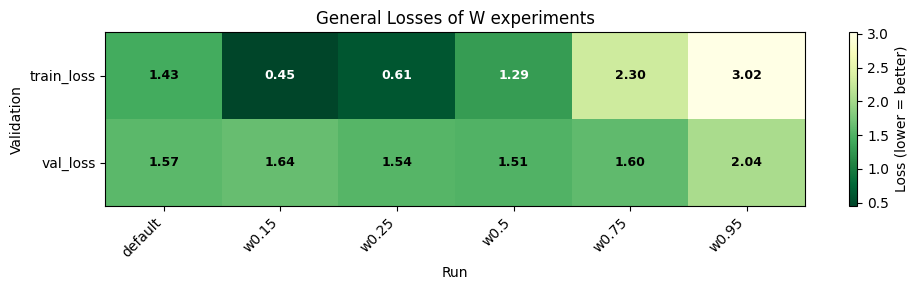It is easier to demask small amount of tokens than many We found that that setting $w$ smaller (in this case $0.15$ and $0.25$) gets us the lowest training losses. This behavior is expected since, with a lower $w$, the model is expected to demask less tokens, which is intuitively much easier to do than having to demask more tokens correctly. But when we look at the validation loss, we see that some masking distribution outperform the default distribution. We see this happening in $w=0.25$ and $w=0.5$, whereas it has a lower validation loss than default

making sure

Yeah that’s great and all but is it really? now i’m not making any bold claims about if it’s a surefire hyperparameter that can make DLM training better, but we’ll look at different validation scenarios, that is, we validate it also on other masking probabilities in our experiments.

We see a more substantial decrease in validation loss (relative to default) when we test these models to demask $0.15 -0.5$ tokens in a given sentence. Surprisingly, $w=0.25$ and $w=0.5$ outperforms the $w=0.15$ model at the $0.15$ validation scheme, suggesting models trained at $w=0.25$ and $w=0.5$ is good at generalizing to demask smaller amount of tokens, even better than models that was specifically trained to demask smaller amounts. However, in our experiments, this phenomenon does not hold beyond $w=0.5$. training to demask more tokens as in $w=0.75$ and $w=0.95$ yields worse validation loss performance, suggesting that there is a diminishing return of the number of tokens to be demasked during training.

variating $\kappa$ experiments

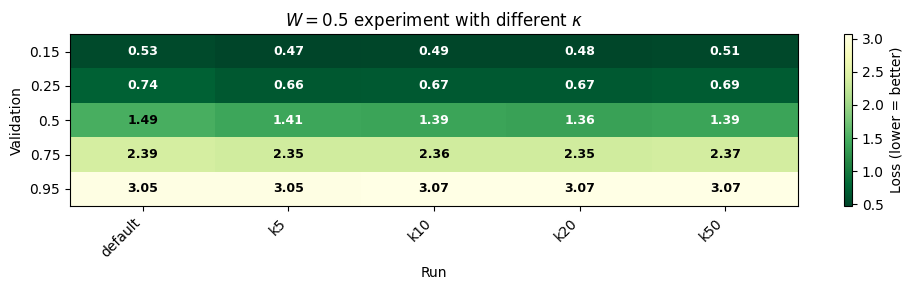We have shown that $w=0.25$ and $w=0.5$ are potential sweet spots of masking probability in DLM training. We further investigated their variance (specifically, we choose $w=0.5$) to dissect this behavior further. We do not conclude any significant behavior when we variate the variance of $w=0.5$. However, we see that all of the $w=0.5$ experiments with different variances all outperform the default distribution, further strengthening our previous hypothesis. This also suggests that expectiation is a more significant variable than variance when it comes to masking probability distribution.

current curriculum learning worsens performance

We found that the our naive curriculum strategy worsens performance despite the intuition of learning to demask smaller amout of tokens in earlier steps would make learning to demask more tokens in later steps easier. Training loss that gradually increases instead of decreasing is expected, since the training task gets harder along with the training steps. However, we make no claims about the performance of curriculum learning in general since this phenomenon warrants further experimentation.

conclusions

We conclude with the suggestion that training DLMs to demask about $0.25-0.5$ work better than the default masking distribution. We further showed that variance in distribution doesn’t really matter. We also see that the current curriculum training doesn’t really work, but we can’t really say that it doesn’t work at all yet, so we still have all the reason to try other fancier way to do curriculum learning.

We release the code on https://github.com/rayendito/dlm_optim

acknowledgements

Many thanks to my colleagues and advisor: Erland Fuadi, Zayd Zuhri, and Dr. Alham Fikri Aji.

references

1. Nie et al (2025), Large Language Diffusion Models

bibtex citation

@misc{diandaru2025dlmabl,
  author       = {Diandaru, Ryandito},
  title        = {Trying Different Probability Distributions for DLM Training and Seeing What Happens},
  year         = {2025},
  howpublished = {\url{https://rayendito.github.io/posts/dlm_ablation}},
}